Using corresponding parts of congruent triangles – In the realm of geometry, the concept of congruent triangles holds significant importance, and at the heart of understanding congruent triangles lies the notion of corresponding parts. This guide delves into the properties, applications, and significance of corresponding parts, providing a comprehensive understanding of their role in proving triangle congruence.
Congruent triangles are triangles that have the same shape and size, meaning their corresponding sides and angles are equal. The properties of congruent triangles include the fact that their corresponding sides are equal in length and their corresponding angles are equal in measure.
Properties of Congruent Triangles: Using Corresponding Parts Of Congruent Triangles
Congruent triangles are triangles that have the same size and shape. This means that their corresponding sides and angles are equal.
The properties of congruent triangles include:
- Corresponding sides are equal.
- Corresponding angles are equal.
- The areas of congruent triangles are equal.
Using Corresponding Parts
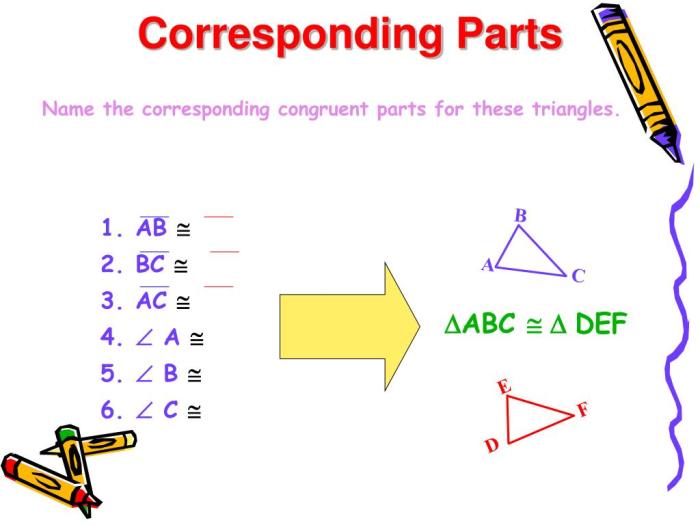
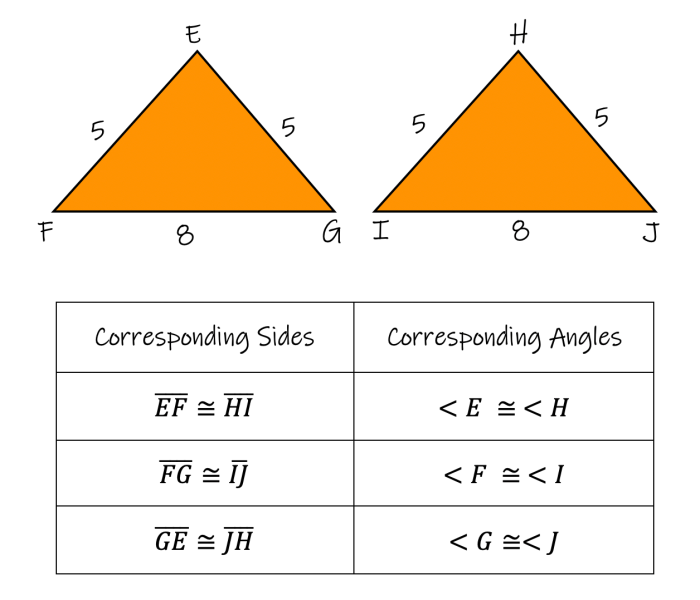
Corresponding parts are the sides and angles that are in the same position in two congruent triangles. For example, the corresponding sides of two congruent triangles are the sides that are opposite the same angle.
Corresponding parts can be used to prove triangles congruent. For example, if two triangles have two pairs of corresponding sides that are equal, then the triangles are congruent.
There are several methods for finding corresponding parts of congruent triangles. One method is to use the angle-side-angle (ASA) congruence theorem. This theorem states that if two triangles have two angles and a side that are equal, then the triangles are congruent.
Another method for finding corresponding parts of congruent triangles is to use the side-side-side (SSS) congruence theorem. This theorem states that if two triangles have three sides that are equal, then the triangles are congruent.
Corresponding parts are significant in geometry because they can be used to prove triangles congruent. This can be useful for solving geometry problems.
Applications of Corresponding Parts
Corresponding parts are used in solving geometry problems. For example, they can be used to find the missing length of a side of a triangle or to find the measure of an angle.
Here are some examples of geometry problems that involve using corresponding parts:
- Find the missing length of the side of a triangle if two sides and an angle are known.
- Find the measure of an angle if two angles and a side are known.
- Prove that two triangles are congruent if three sides or two sides and an angle are known.
The following table summarizes the applications of corresponding parts:
| Application | Example |
|---|---|
| Find the missing length of a side of a triangle | If two sides and an angle are known, then the missing length of the side can be found using the Pythagorean theorem. |
| Find the measure of an angle | If two angles and a side are known, then the measure of the angle can be found using the angle sum property of triangles. |
| Prove that two triangles are congruent | If three sides or two sides and an angle are known, then the triangles can be proven congruent using the SSS congruence theorem or the ASA congruence theorem. |
Visual Representations, Using corresponding parts of congruent triangles
Diagrams can be used to illustrate the use of corresponding parts. For example, the following diagram shows two congruent triangles:

The corresponding sides of the triangles are labeled with the same letters. The corresponding angles are labeled with the same Greek letters.
The following table summarizes the key points about corresponding parts:
- Corresponding sides are equal.
- Corresponding angles are equal.
- Corresponding parts can be used to prove triangles congruent.
- Corresponding parts are significant in geometry because they can be used to solve geometry problems.
FAQ Overview
What are corresponding parts of congruent triangles?
Corresponding parts are pairs of sides or angles in congruent triangles that occupy the same relative positions.
How can corresponding parts be used to prove triangles congruent?
Corresponding parts can be used to prove triangles congruent by showing that the corresponding sides and angles are equal.
What is the significance of using corresponding parts in geometry?
Using corresponding parts in geometry allows for the efficient and accurate determination of triangle congruence, which is essential for solving a wide range of geometric problems.